Misay's blog

MoeCTF2025

发表于 更新于 分类于
MoeCTF2025-Crypto-WP

Intro

比赛地址https://ctf.xidian.edu.cn/

很棒的新生赛，去年这个时候还看不懂题，今年成功akCrypto了 大致本文就密码方向的题来进行一个Write的Up

Challenge

密码学入门指北

ElGamal非对称 给你了私钥 如下计算

exp

1
2
3
4
5
6
7
8
9
10
11
p =
g = 2
y =
c1 =
c2 =
x =
from Crypto.Util.number import long_to_bytes
S=pow(c1,x,p)
m = inverse_mod(S,p) * c2 % p
print(long_to_bytes(m))
# b'moectf{th1s_1s_y0ur_f1rst_ElG@m@l}'

ez_DES

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from Crypto.Cipher import DES
import secrets
import string

flag = 'moectf{???}'
characters = string.ascii_letters + string.digits + string.punctuation
key = 'ezdes'+''.join(secrets.choice(characters) for _ in range(3))
assert key[:5] == 'ezdes'
key = key.encode('utf-8')
l = 8

def encrypt(text, key):
    cipher = DES.new(key, DES.MODE_ECB)
    padded_text = text + (l - len(text) % l) * chr(len(text))
    data = cipher.encrypt(padded_text.encode('utf-8'))
    return data

c = encrypt(flag, key)
print('c =', c)

# c = b'\xe6\x8b0\xc8m\t?\x1d\xf6\x99sA>\xce \rN\x83z\xa0\xdc{\xbc\xb8X\xb2\xe2q\xa4"\xfc\x07'

DES作为一组对称的分组密码 使用相同的密钥进行加密解密 密钥组成是”ezdes???“我们直接穷举爆破密钥即可

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
from Crypto.Cipher import DES
import string

# Provided ciphertext
c = b'\xe6\x8b0\xc8m\t?\x1d\xf6\x99sA>\xce \rN\x83z\xa0\xdc{\xbc\xb8X\xb2\xe2q\xa4"\xfc\x07'

# The character set used for the variable part of the key
characters = string.ascii_letters + string.digits + string.punctuation
known_prefix = 'ezdes'
known_flag_prefix = b'moectf{'

print("[*] Starting brute-force attack on the DES key...")

# 1. Generate all possible keys
for char1 in characters:
    for char2 in characters:
        for char3 in characters:
            # Construct the candidate key
            suffix = char1 + char2 + char3
            key = (known_prefix + suffix).encode('utf-8')

            # 2. Attempt to decrypt the ciphertext with the candidate key
            try:
                cipher = DES.new(key, DES.MODE_ECB)
                decrypted_data = cipher.decrypt(c)

                # 3. Check if the decrypted data starts with the known flag prefix
                if decrypted_data.startswith(known_flag_prefix):
                    print(f"\n[+] Success! Key found: {key}")
                    
                    # The decrypted data includes padding, we need to remove it.
                    # The padding byte value is the original length of the flag.
                    # The last byte of the padded text is this value.
                    original_len = decrypted_data[-1]
                    flag = decrypted_data[:original_len]
                    
                    print(f"[+] Decrypted Flag: {flag.decode()}")
                    
                    # Exit the script once the flag is found
                    exit(0)

            except Exception:
                # Ignore errors from invalid keys/padding during decryption
                continue

# moectf{_Ju5t envmEra+e.!}

实际上多个不同的key都能解出一样的flag

baby-next

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from Crypto.Util.number import *
from gmpy2 import next_prime
from functools import reduce
from secret import flag

assert len(flag) == 38
assert flag[:7] == b'moectf{'
assert flag[-1:] == b'}'

def main():
    p = getPrime(512)
    q = int(reduce(lambda res, _: next_prime(res), range(114514), p))

    n = p * q
    e = 65537

    m = bytes_to_long(flag)

    c = pow(m, e, n)

    print(f'{n = }')
    print(f'{c = }')

if __name__ == '__main__':
    main()

是随机512位素数 是后的下一个素数 直接搜索即可 这个数量级我们基本就有 exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
from Crypto.Util.number import long_to_bytes, inverse
from gmpy2 import isqrt, is_square

n = 
c = 
e = 

s = isqrt(n)

if s * s < n:
    s += 1

iterations = 0
while True:
    d_squared = s * s - n
    if is_square(d_squared):
        d = isqrt(d_squared)
        p = s - d
        q = s + d
        print(f"[+] 成功分解 n! (在 {iterations} 次迭代后)")
        print(f"p = {p}")
        print(f"q = {q}")
        break
    
    s += 1
    iterations += 1
    if iterations % 100000 == 0: 
        print(f"[*] 已迭代 {iterations} 次, 当前 s: {s}")

# --- 标准 RSA 解密 ---
assert p * q == n

phi = (p - 1) * (q - 1)
d = inverse(e, phi)
m = pow(c, d, n)

flag = long_to_bytes(m)
print("\n[+] 解密成功!")
print(f"[*] Flag: {flag.decode()}")

# moectf{vv0W_p_m1nu5_q_i5_r34l1y_sm4lI}

ezBSGS

即求解DLP sagemath有自带模数域下的离散对数方法 这里可以直接用

1
2
3
4
5
6
7
8
9
a = 13
b = 114514
p = 100000000000099
F = GF(p)
a = F(a)
b = F(b)
x = discrete_log(b,a)
print(x)
# 18272162371285

说回BSGS算法本身 是一种用空间换时间的搜索策略

对于生成元为,模的乘法群，当为素数 我们想求解离散对数问题 我们把想求的设为 其中 是当前群的阶，我们想找到实际上搜索上界是

我们有 注意到都是相对独立的，我们可以提前计算好所有的 然后对所有的 我们都可以计算，查哈希表 即可

ez_square

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from Crypto.Util.number import *
from secret import flag

assert len(flag) == 35
assert flag[:7] == b'moectf{'
assert flag[-1:] == b'}'

def main():
    p = getPrime(512)
    q = getPrime(512)

    n = p * q
    e = 65537

    m = bytes_to_long(flag)

    c = pow(m, e, n)
    hint = pow(p + q, 2, n)

    print(f'{n = }')
    print(f'{c = }')
    print(f'{hint = }')

if __name__ == '__main__':
    main()

我们需要解形似 的丢番图方程 sagemath实际上有对应的方法 貌似Mini-L CTF和DASCTF2024-8都出过这种的 exp如下

方法比较多 我们来讲几个经典的

首先我们的RSA解密加密都是在模环上进行的 我们可以用代掉 考虑构造一个解 的方程 利用对称性来解 这里就和给出 我觉得是没有区别的

其余方法如下

sagemath里面有这种判断并且恢复的平方和分解的接口two_squares(),源码大致如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
cdef int two_squares_c(uint_fast32_t n, uint_fast32_t res[2]) noexcept:
    r"""
    Return ``1`` if ``n`` is a sum of two squares and ``0`` otherwise.

    If ``1`` is returned, the value of ``res[0]`` and ``res[1]`` are set to the
    lexicographically smallest solution of `a^2 + b^2 = n`.
    """
    cdef uint_fast32_t fac,i,ii,j,jj,nn

    if n == 0:
        res[0] = res[1] = 0
        return 1

    # if n = 0 mod 4 then i and j must be even
    # hence, we first remove the maximum power of 4 from n and will then
    # multiply by the corresponding power of 2 the solution
    fac = 0
    while n % 4 == 0:
        n >>= 2
        fac += 1

    # now, n is congruent to 1,2 or 3 mod 4.
    # As a square is congruent to 0,1 mod 4, a sum of square is congruent to
    # 0,1,2 mod 4.
    if n % 4 == 3:
        return 0

    # if n=1 mod 4 then exactly one of i or j must be even
    # if n=2 mod 4 then i and j must be odd
    if n % 4 == 1:
        i = ii = 0
        j = <uint_fast32_t> sqrt(<double> n)
        jj = j*j
        while ii <= jj:
            nn = n - ii
            while jj > nn:
                j -= 1
                # strangely enough, the 1-by-1 decreasing above is much faster
                # than integer Newton iteration:
                # j = (j+nn/j)/2
                jj = j*j
            if jj == nn:
                res[0] = i<<fac
                res[1] = j<<fac
                return 1
            i += 1
            ii = i*i
    else: # n mod 4 = 2
        i = ii = 1
        j = <uint_fast32_t> sqrt(<double> n)
        j += 1 - j % 2
        jj = j*j
        while ii <= jj:
            nn = n - ii
            while jj > nn:
                j -= 2
                # strangely enough, the 2-by-2 decreasing above is much faster
                # than integer Newton iteration:
                # j = (j+nn/j)/2
                jj = j*j
            if jj == nn:
                res[0] = i<<fac
                res[1] = j<<fac
                return 1
            i += 2
            ii = i*i

    return 0

大致思路是任何形如的数无法表示为两个数的平方和，通过这种方式来实现快速剪枝，分类讨论 的情况，在大小相近的时候能够快速的返回答案，因此很适合RSA问题

同时还存在一种复数域下的因数分解

还想到另一种在高斯整数环（复数域）下的分解 下面的exp还是最简单的解方程的手法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
n = 83917281059209836833837824007690691544699901753577294450739161840987816051781770716778159151802639720854808886223999296102766845876403271538287419091422744267873129896312388567406645946985868002735024896571899580581985438021613509956651683237014111116217116870686535030557076307205101926450610365611263289149
c = 69694813399964784535448926320621517155870332267827466101049186858004350675634768405333171732816667487889978017750378262941788713673371418944090831542155613846263236805141090585331932145339718055875857157018510852176248031272419248573911998354239587587157830782446559008393076144761176799690034691298870022190
hint = 5491796378615699391870545352353909903258578093592392113819670099563278086635523482350754035015775218028095468852040957207028066409846581454987397954900268152836625448524886929236711403732984563866312512753483333102094024510204387673875968726154625598491190530093961973354413317757182213887911644502704780304
# P.<x> = PolynomialRing(Zmod(n))
# f = x^4 + n^2 - hint * x^2
# res = f.small_roots(X = 2^512, beta = 0.65, epsilon = 0.01)
# print(res)

from Crypto.Util.number import long_to_bytes, inverse
from gmpy2 import is_square, isqrt

e = 65537

# --- 2. 求解 p+q 的确切值 S ---
S_squared_candidate = 0
found_k = False

# 尝试 k 的几个小整数值，根据我们的估算，k=4 的可能性最大
for k in range(1, 10):
    print(f"[*] 正在尝试 k = {k}...")
    candidate = k * n + hint
    # 检查 k*n + hint 是否为完全平方数
    if is_square(candidate):
        S_squared_candidate = candidate
        print(f"[+] 成功! 当 k = {k} 时, k*n + hint 是一个完全平方数。")
        found_k = True
        break

if not found_k:
    print("[-] 求解 S^2 失败，未找到合适的 k。")
    exit()

# S 就是 p+q
S = isqrt(S_squared_candidate)
print(f"\n[*] 计算得到 p+q 的值:")
print(f"S = {S}")
print("-" * 30)


# --- 3. 求解一元二次方程 x^2 - S*x + n = 0 来分解 n ---
# 判别式 delta = S^2 - 4n
delta = S**2 - 4 * n

if delta < 0 or not is_square(delta):
    print("[-] 判别式无效，无法分解 n。")
    exit()

# p, q = (S ± sqrt(delta)) / 2
sqrt_delta = isqrt(delta)
p = (S + sqrt_delta) // 2
q = (S - sqrt_delta) // 2

# 验证分解是否正确
if p * q == n:
    print("[+] 成功分解 n!")
    print(f"{p = }")
    print(f"{q = }")
    print("-" * 30)
else:
    print("[-] 分解 n 失败，p*q 不等于 n。")
    exit()


# --- 4. 标准 RSA 解密流程 ---
phi = (p - 1) * (q - 1)
d = inverse(e, phi)
m = pow(c, d, n)

flag = long_to_bytes(m)

print("[+] 解密成功!")
print(f"[*] Flag (bytes): {flag}")
print(f"[*] Flag (string): {flag.decode()}")

# b'moectf{Ma7hm4t1c5_is_@_k1nd_0f_a2t}'

直接造方程也可以 这里是简单搜索出 没有本质区别

ez_AES

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
from secret import flag

rc = [0x12, 0x23, 0x34, 0x45, 0x56, 0x67, 0x78, 0x89, 0x9a, 0xab, 0xbc, 0xcd, 0xde, 0xef,0xf1]

s_box = [
	[0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76],
	[0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0],
	[0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15],
	[0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75],
	[0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84],
	[0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf],
	[0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8],
	[0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2],
	[0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73],
	[0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb],
	[0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79],
	[0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08],
	[0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a],
	[0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e],
	[0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf],
	[0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16]
]

s_box_inv = [
	[0x52, 0x09, 0x6a, 0xd5, 0x30, 0x36, 0xa5, 0x38, 0xbf, 0x40, 0xa3, 0x9e, 0x81, 0xf3, 0xd7, 0xfb],
	[0x7c, 0xe3, 0x39, 0x82, 0x9b, 0x2f, 0xff, 0x87, 0x34, 0x8e, 0x43, 0x44, 0xc4, 0xde, 0xe9, 0xcb],
	[0x54, 0x7b, 0x94, 0x32, 0xa6, 0xc2, 0x23, 0x3d, 0xee, 0x4c, 0x95, 0x0b, 0x42, 0xfa, 0xc3, 0x4e],
	[0x08, 0x2e, 0xa1, 0x66, 0x28, 0xd9, 0x24, 0xb2, 0x76, 0x5b, 0xa2, 0x49, 0x6d, 0x8b, 0xd1, 0x25],
	[0x72, 0xf8, 0xf6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xd4, 0xa4, 0x5c, 0xcc, 0x5d, 0x65, 0xb6, 0x92],
	[0x6c, 0x70, 0x48, 0x50, 0xfd, 0xed, 0xb9, 0xda, 0x5e, 0x15, 0x46, 0x57, 0xa7, 0x8d, 0x9d, 0x84],
	[0x90, 0xd8, 0xab, 0x00, 0x8c, 0xbc, 0xd3, 0x0a, 0xf7, 0xe4, 0x58, 0x05, 0xb8, 0xb3, 0x45, 0x06],
	[0xd0, 0x2c, 0x1e, 0x8f, 0xca, 0x3f, 0x0f, 0x02, 0xc1, 0xaf, 0xbd, 0x03, 0x01, 0x13, 0x8a, 0x6b],
	[0x3a, 0x91, 0x11, 0x41, 0x4f, 0x67, 0xdc, 0xea, 0x97, 0xf2, 0xcf, 0xce, 0xf0, 0xb4, 0xe6, 0x73],
	[0x96, 0xac, 0x74, 0x22, 0xe7, 0xad, 0x35, 0x85, 0xe2, 0xf9, 0x37, 0xe8, 0x1c, 0x75, 0xdf, 0x6e],
	[0x47, 0xf1, 0x1a, 0x71, 0x1d, 0x29, 0xc5, 0x89, 0x6f, 0xb7, 0x62, 0x0e, 0xaa, 0x18, 0xbe, 0x1b],
	[0xfc, 0x56, 0x3e, 0x4b, 0xc6, 0xd2, 0x79, 0x20, 0x9a, 0xdb, 0xc0, 0xfe, 0x78, 0xcd, 0x5a, 0xf4],
	[0x1f, 0xdd, 0xa8, 0x33, 0x88, 0x07, 0xc7, 0x31, 0xb1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xec, 0x5f],
	[0x60, 0x51, 0x7f, 0xa9, 0x19, 0xb5, 0x4a, 0x0d, 0x2d, 0xe5, 0x7a, 0x9f, 0x93, 0xc9, 0x9c, 0xef],
	[0xa0, 0xe0, 0x3b, 0x4d, 0xae, 0x2a, 0xf5, 0xb0, 0xc8, 0xeb, 0xbb, 0x3c, 0x83, 0x53, 0x99, 0x61],
	[0x17, 0x2b, 0x04, 0x7e, 0xba, 0x77, 0xd6, 0x26, 0xe1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0c, 0x7d]
]

def sub_bytes(grid):
    for i, v in enumerate(grid):
        grid[i] = s_box[v >> 4][v & 0xf]

def shift_rows(grid):
    for i in range(4):
        grid[i::4] = grid[i::4][i:] + grid[i::4][:i]
        grid =grid[0::4]+grid[1::4]+grid[2::4]+grid[3::4]

def mix_columns(grid):
    def mul_by_2(n):
        s = (n << 1) & 0xff
        if n & 128:
            s ^= 0x1b
        return s

    def mul_by_3(n):
        return n ^ mul_by_2(n)

    def mix_column(c):
        return [
            mul_by_2(c[0]) ^ mul_by_3(c[1]) ^ c[2] ^ c[3],  # [2 3 1 1]
	    c[0] ^ mul_by_2(c[1]) ^ mul_by_3(c[2]) ^ c[3],  # [1 2 3 1]
	    c[0] ^ c[1] ^ mul_by_2(c[2]) ^ mul_by_3(c[3]),  # [1 1 2 3]
	    mul_by_3(c[0]) ^ c[1] ^ c[2] ^ mul_by_2(c[3]),  # [3 1 1 2]
	]

    for i in range(0, 16, 4):
        grid[i:i + 4] = mix_column(grid[i:i + 4])

def key_expansion(grid):
    for i in range(10 * 4):
        r = grid[-4:]
        if i % 4 == 0:  # 对上一轮最后4字节自循环、S-box置换、轮常数异或，从而计算出当前新一轮最前4字节
            for j, v in enumerate(r[1:] + r[:1]):
                r[j] = s_box[v >> 4][v & 0xf] ^ (rc[i // 4] if j == 0 else 0)

        for j in range(4):
            grid.append(grid[-16] ^ r[j])

    return grid

def add_round_key(grid, round_key):
    for i in range(16):
        grid[i] ^= round_key[i]

def encrypt(b, expanded_key):
    # First round
    add_round_key(b, expanded_key)

    for i in range(1, 10):
        sub_bytes(b)
        shift_rows(b)
        mix_columns(b)
        add_round_key(b, expanded_key[i * 16:])

    # Final round
    sub_bytes(b)
    shift_rows(b)
    add_round_key(b, expanded_key[-16:])
    return b


def aes(key, msg):
    expanded = key_expansion(bytearray(key))

    # Pad the message to a multiple of 16 bytes
    b = bytearray(msg + b'\x00' * (16 - len(msg) % 16))
    # Encrypt the message
    for i in range(0, len(b), 16):
        b[i:i + 16] = encrypt(b[i:i + 16], expanded)
    return bytes(b)

if __name__ == '__main__':
    key = b'Slightly different from the AES.'
    enc = aes(key, flag)

    print('Encrypted:', enc)
    #Encrypted: b'%\x98\x10\x8b\x93O\xc7\xf02F\xae\xedA\x96\x1b\xf9\x9d\x96\xcb\x8bT\r\xd31P\xe6\x1a\xa1j\x0c\xe6\xc8'

简化后的AES对称 直接交给GPT梭了

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
from Crypto.Util.number import *
from Crypto.Cipher import AES
import gmpy2
import string

# Given data from the problem
lis0 = [[341, 710, 523, 1016], [636, 366, 441, 790], [637, 347, 728, 426], [150, 184, 421, 733]]
lis1 = [[133, 301, 251, 543], [444, 996, 507, 1005], [18, 902, 379, 878], [235, 448, 836, 263]]
text_val = 26588763961966808496088145486940545448967891102453278501457496293530671899568
a = [[239, 239, 251, 239], [233, 227, 233, 251], [251, 239, 251, 233], [233, 227, 251, 233]]
p_ = 71583805456773770888820224577418671344500223401233301642692926000191389937709
p = 251

# Step 1: Recover final ciphertext state
final_text_long1 = pow(text_val, (p_ + 1) // 4, p_)
final_text_long2 = p_ - final_text_long1
try:
    final_text = long_to_bytes(final_text_long1, 32)
except ValueError:
    final_text = long_to_bytes(final_text_long2, 32)
text_final_0 = final_text[:16]
text_final_1 = final_text[16:]

# Helper functions for decryption logic
def function(x, p_local):
    if x >= p_local: return x
    if pow(x, (p_local - 1) // 2, p_local) == 1: return pow(x, 2, p_local)
    else: return pow(x, 3, p_local)

S = {function(x, p) for x in range(256)}

def inv_function_251(y):
    if y >= p: return y
    leg = gmpy2.legendre(y, p)
    if leg == 1:
        s1 = pow(y, (p + 1) // 4, p)
        s2 = p - s1
        return s1 if gmpy2.legendre(s1, p) == 1 else s2
    elif leg == -1: return pow(y, gmpy2.invert(3, p - 1), p)
    else: return 0

def solve_half(cipher, current_text, lis, a_mat):
    for i in range(9, -1, -1):
        T = [[current_text[r + 4*c] for r in range(4)] for c in range(4)]
        M = [[0]*4 for _ in range(4)]
        for r in range(4):
            for c in range(4):
                y_target = T[c][r]
                p_local = a_mat[r][c]
                bit = (lis[r][c] >> (9 - i)) & 1
                for x_cand in S:
                    if function(x_cand, p_local) == y_target and ((x_cand > p_local // 2) == bit):
                        M[r][c] = x_cand
                        break
        enc_bytes = bytearray(16)
        for r in range(4):
            for c in range(4):
                enc_bytes[r + 4*c] = inv_function_251(M[r][c])
        current_text = cipher.decrypt(bytes(enc_bytes))
    return current_text

# Step 2 & 3: Brute-force the 16-bit key and decrypt
for key_int in range(2**16):
    if key_int % 1000 == 0:
        print(f"[*] Trying key: {key_int}")

    aes_key = long_to_bytes(key_int << 107, 16)
    cipher = AES.new(aes_key, AES.MODE_ECB)

    try:
        flag0 = solve_half(cipher, text_final_0, lis0, a)
        flag1 = solve_half(cipher, text_final_1, lis1, a)
        flag = flag0 + flag1
        
        # Check if the result is a printable flag
        if all(c in string.printable.encode() for c in flag):
            print(f"\n[+] Found Key: {key_int}")
            print(f"[+] Flag: flag{{{flag.decode()}}}")
            break
    except Exception:
        continue
        
 # b'moectf{Th1s_1s_4n_E4ZY_AE5_!@#}\x00'

ez_det

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
from random import randrange
from Crypto.Util.number import *
from sage.all import*
from secret import flag


m_blocks = [bytes_to_long(flag), 0, 0, 0, 0]
p = getPrime(128)

def make_mask(n, p):
    upper = identity_matrix(n)
    low   = identity_matrix(n)
    for i in range(n-1):
        for j in range(i+1, n):
            upper[i, j] = randrange(1, p)
            low[j, i]   = randrange(1, p)
    result = upper * low
    assert det(result) == 1
    return result

def matrix_to_list(mat):
    return [list(row) for row in mat]

Noise = [[randrange(1, p) for _ in range(5)] for _ in range(4)]
Noise.append(m_blocks)

M = matrix(Noise)
A = make_mask(5, p)
C = A * M

print(f"Noise1={Noise[:4]}")
print(f"C={matrix_to_list(C)}")

给出的明文矩阵形似 前四行是没有用的noise 后一行的第一列是我们的flag

给出密文矩阵 且保证 我们分析这里的代数结构

Step 1: 利用后 4 列恢复 ( A ) 的前 4 列

观察 ( M ) 的后 4 列（列 1~4，索引从 0 开始）： - 第 5 行全为 0 - 所以前 4 行构成了一个 4×4 子矩阵 ，且已知

设：（后 4 列）;（前 4 行，后 4 列）

由于，所以：

但由于是 5×4 矩阵，第 5 行为 0。

因此，后 4 列的乘法实际上只涉及的前列！
令 (5×4），则： 其中 是 4×4 可逆矩阵（题中已保证 det ≠ 0）。

于是可解：

Step 2: 利用第一列关系提取含向量

现在看的第一列（对应的第一列）：

移项得： 令右边为向量，即： 此时我们有：（5×4）; ，其中 是 的第 5 列

Step 3: 构造矩阵 ，并计算行列式

现在构造新矩阵：

但 ，所以有 根据行列式性质：

而题目中 make_mask 保证了： 因此： exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80

Noise1 = 
C_list = 


C_mat = matrix(C_list)
M_known_rows = matrix(Noise1)


# 3. 步骤 1: 恢复密钥矩阵 A 的前四列 (A_sub)
# ----------------------------------------------
# C_sub = A_sub * M_sub  =>  A_sub = C_sub * M_sub^(-1)

# 构造 C_sub (C 的后四列)
C_sub = C_mat.matrix_from_columns([1, 2, 3, 4])

# 构造 M_sub (已知Noise的前4行和后4列)
M_sub = M_known_rows.matrix_from_columns([1, 2, 3, 4])

# 确保 M_sub 可逆
if M_sub.det() == 0:
    print("❌ 错误: M_sub 矩阵不可逆，无法继续。")
else:
    print("🔄 正在计算 M_sub 的逆矩阵...")
    # 在有理数域 QQ 上计算逆矩阵
    M_sub_inv = M_sub.change_ring(QQ)^-1

    # 计算 A_sub
    A_sub = C_sub.change_ring(QQ) * M_sub_inv
    print("✅ 成功恢复 A 的前四列 (A_sub)。\n")


    # 4. 步骤 2: 利用第一列关系计算向量 v
    # ------------------------------------
    # v = c_1 - (m_11*a_1 + m_21*a_2 + m_31*a_3 + m_41*a_4)
    # 这等价于 v = c_1 - A_sub * m_col1

    # 提取 c_1 (C 的第一列)
    c1_vec = C_mat.column(0)

    # 提取 M 的已知部分的第一列
    m_known_col1 = M_known_rows.column(0)

    # 计算 v
    print("🔄 正在计算向量 v...")
    v_vec = c1_vec - A_sub * m_known_col1
    print("✅ 向量 v 计算完成。\n")


    # 5. 步骤 3: 构造矩阵 A' 并计算其行列式得到 m
    # --------------------------------------------
    # A' = [a_1, a_2, a_3, a_4, v]
    # m = det(A')

    # 构造 A'
    # 使用 augment 方法将 v_vec 作为新的一列附加到 A_sub 后面
    A_prime = A_sub.augment(v_vec)

    print("🔄 正在计算最终行列式以求解 m...")
    # 计算行列式
    m = A_prime.det()
    
    # 结果应该是整数
    m = Integer(m)
    print(f"✅ 成功解出 m!\n")
    print(f"m (整数形式) = {m}\n")


    # 6. 将 m 转换回 flag 字符串
    # ---------------------------
    from Crypto.Util.number import long_to_bytes

    try:
        flag = long_to_bytes(m)
        print("🎉🎉🎉 最终 Flag: 🎉🎉🎉")
        print(flag.decode())
    except Exception as e:
        print(f"❌ 转换 flag 失败: {e}")
        
  # moectf{D0_Y0u_kn0w_wh@7_4_de7erm1n@n7_1s!}

ezlegendre

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from Crypto.Util.number import getPrime, bytes_to_long
from secret import flag

p = 258669765135238783146000574794031096183
a = 144901483389896508632771215712413815934

def encrypt_flag(flag):
    ciphertext = []
    plaintext = ''.join([bin(i)[2:].zfill(8) for i in flag])
    for b in plaintext:
        e = getPrime(16)
        d = randint(1,10)
        n = pow(a+int(b)*d, e, p)
        ciphertext.append(n)
    return ciphertext

print(encrypt_flag(flag))

和去年的一样 利用二次剩余逐比特恢复即可

当为0

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

from Crypto.Util.number import long_to_bytes
import gmpy2


p = 258669765135238783146000574794031096183
a = 144901483389896508632771215712413815934

ciphertext = 

assert gmpy2.legendre(a, p) == 1,

# --- 解密过程 ---

binary_flag = ""
print("[*] 开始解密每一位...")

for i, n in enumerate(ciphertext):
    # 计算每个密文 n 对于 p 的勒让德符号
    legendre_symbol = gmpy2.legendre(n, p)
    
    if legendre_symbol == 1:
        # 如果 n 是二次剩余，我们推断原始比特是 0
        binary_flag += '0'
    elif legendre_symbol == -1:
        # 如果 n 是二次非剩余，我们推断原始比特是 1
        binary_flag += '1'
    else:
        # 这种情况基本不会发生
        print(f"[!] 警告: 密文 {i} (值为 {n}) 对于 p 的勒让德符号为 0，这意味着 n 是 p 的倍数。")
        # 可以根据情况决定如何处理，例如添加 '?'
        binary_flag += '?'

print("\n[*] 解密完成!")
print(f"[*] 恢复的二进制flag序列: {binary_flag}")
print("-" * 30)


# --- 将二进制序列转换回 flag ---

# 检查二进制序列长度是否为8的倍数
if len(binary_flag) % 8 != 0:
    print(f"[!] 警告: 恢复的二进制序列长度 {len(binary_flag)} 不是8的倍数，转换可能有误。")

# 将二进制字符串每8位进行切割，转换为整数，再转换为字节
try:
    flag_bytes = long_to_bytes(int(binary_flag, 2))
    print(f"[+] 成功恢复FLAG: {flag_bytes.decode()}")
except Exception as e:
    print(f"[-] 转换flag失败: {e}")
    
# moectf{Y0u_h@v3_ju5t_s01v3d_7h1s_pr0b13m!}

ChallengeMore

杂交随机数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
from Crypto.Util.number import bytes_to_long

def lfsr(data, mask):
    mask = mask.zfill(len(data))
    res_int = int(data, base=2)^int(mask, base=2)
    bit = 0
    while res_int > 0:
        bit ^= res_int % 2
        res_int >>= 1

    res = data[1:]+str(bit)
    return res

def lcg(x, a, b, m):
    return (a*x+b)%m

flag = b'moectf{???}'

x = bin(bytes_to_long(flag))[2:].zfill(len(flag)*8)
l = len(x)//2
L, R = x[:l], x[l:]
b = -233
m = 1<<l

for _ in range(2025):
    mask = R
    seed = int(L, base=2)
    L = lfsr(L, mask)
    R = bin(lcg(int(R, base=2), b, seed, m))[2:].zfill(l)
    L, R = R, L

en_flag = L+R
print(int(en_flag, base=2))
# en_flag = 4567941593066862873653209393990031966807270114415459425382356207107640

杂糅lcg与lfsr的prng，我们梳理一下逻辑

是flag转二进制补全到8的倍数长，随后分成L R两个块

m是一个掩码位，b是参数 给lcg用的，随后用R对L进行LFSR处理，R自身进行一个LCG，seed是原本的L,随后交换LR，最后告诉你末态

lsfr

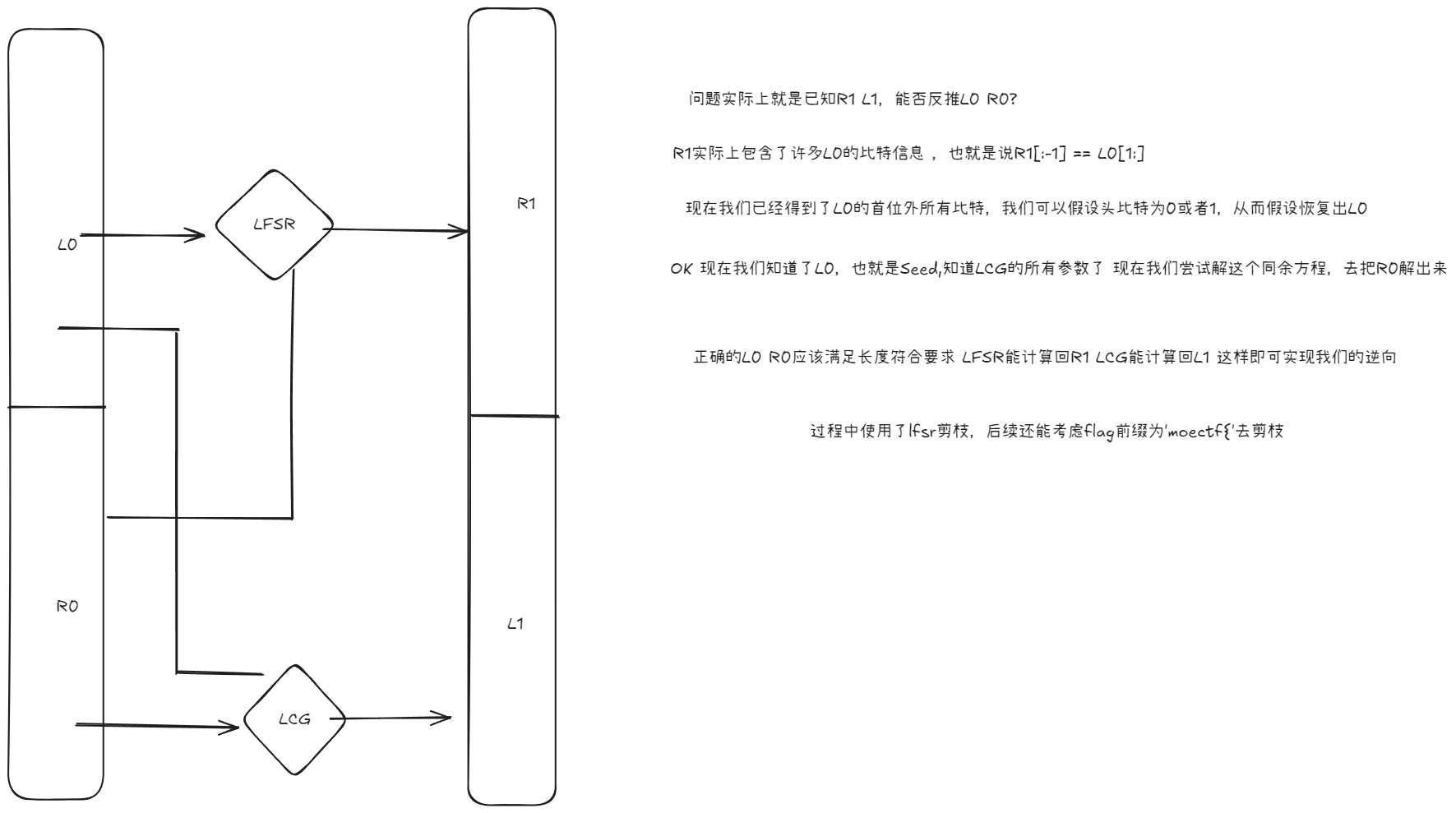
DFS剪枝的脚本by GPT5老师

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
# Using prefix pruning: Deepening the bounded DFS and random trials with known prefix 'moectf{'.
# We'll try a larger DFS node budget (1,000,000) and more random trials (50,000).
# If a candidate is found whose initial bytes start with the prefix, we'll print it.

from Crypto.Util.number import long_to_bytes
import random, time

en_flag = 4567941593066862873653209393990031966807270114415459425382356207107640
flag_len = 29
bit_len = flag_len * 8
l = bit_len // 2
m = 1 << l
b_coef = -233
ROUNDS = 2025

PREFIX = b"moectf{"

def lfsr(data, mask):
    mask = mask.zfill(len(data))
    res_int = int(data, 2) ^ int(mask, 2)
    bit = 0
    while res_int > 0:
        bit ^= res_int & 1
        res_int >>= 1
    return data[1:] + str(bit)

def lcg(x, a, b, m):
    return (a * x + b) % m

def inverse_round_candidates(L_curr, R_curr):
    L_next, R_next = R_curr, L_curr
    candidates = []
    a_mod = b_coef % m
    inv_a = pow(a_mod, -1, m)
    for first_bit in (0,1):
        preL = str(first_bit) + L_next[:-1]
        preL_int = int(preL, 2)
        rhs = (int(R_next,2) - preL_int) % m
        preR_int = (rhs * inv_a) % m
        preR = bin(preR_int)[2:].zfill(l)
        # verify forward
        if lfsr(preL, preR) == L_next and bin(lcg(preR_int, b_coef, preL_int, m))[2:].zfill(l) == R_next:
            candidates.append((preL, preR))
    return candidates

# initial state from en_flag
x = bin(en_flag)[2:].zfill(bit_len)
startL, startR = x[:l], x[l:]

# Bounded DFS with prefix final-check
def bounded_dfs_with_prefix(max_nodes = 1000000, verbose=True):
    stack = [(startL, startR, 0)]
    nodes = 0
    t0 = time.time()
    while stack and nodes < max_nodes:
        currL, currR, done = stack.pop()
        nodes += 1
        if done == ROUNDS:
            origin_bytes = long_to_bytes(int(currL + currR, 2))
            if origin_bytes.startswith(PREFIX):
                return origin_bytes, nodes
            else:
                continue
        cands = inverse_round_candidates(currL, currR)
        if not cands:
            continue
        # push candidates: push the one with first_bit=0 first or last? keep both.
        for preL, preR in cands:
            stack.append((preL, preR, done+1))
        if verbose and nodes % 50000 == 0:
            print(f"... DFS nodes={nodes}, stack={len(stack)}, elapsed={time.time()-t0:.2f}s, progress_done={done}")
    return None, nodes

# Random trials: select random valid preimages at branches, check final prefix
def random_trials_with_prefix(num_trials=50000):
    t0 = time.time()
    for t in range(num_trials):
        currL, currR = startL, startR
        ok = True
        for i in range(ROUNDS):
            cands = inverse_round_candidates(currL, currR)
            if not cands:
                ok = False
                break
            currL, currR = random.choice(cands)
        if ok:
            origin_bytes = long_to_bytes(int(currL + currR, 2))
            if origin_bytes.startswith(PREFIX):
                return origin_bytes, t+1
        if (t+1) % 5000 == 0:
            print("random trials:", t+1, "elapsed", time.time()-t0)
    return None, num_trials

# Run DFS then random trials
print("Starting bounded DFS (node limit 1,000,000) with prefix check...")
res_dfs, nodes_used = bounded_dfs_with_prefix(1000000, verbose=True)
print("DFS finished. result:", res_dfs, "nodes_used:", nodes_used)

if res_dfs is None:
    print("Starting random trials (50,000) with prefix check...")
    res_rand, trials_done = random_trials_with_prefix(50000)
    print("Random trials finished. result:", res_rand, "trials_done:", trials_done)
else:
    print("Found by DFS, skipping random trials.")

# Print final summary
if res_dfs is not None:
    print("\n=== FOUND by DFS ===\n", res_dfs)
elif 'res_rand' in locals() and res_rand is not None:
    print("\n=== FOUND by random trials ===\n", res_rand)
else:
    print("\nNo flag found with prefix-based search within these budgets.")

'''
Starting bounded DFS (node limit 1,000,000) with prefix check...
... DFS nodes=50000, stack=361, elapsed=0.87s, progress_done=695
... DFS nodes=100000, stack=431, elapsed=1.79s, progress_done=839
... DFS nodes=150000, stack=451, elapsed=2.66s, progress_done=857
... DFS nodes=250000, stack=751, elapsed=4.37s, progress_done=1499
... DFS nodes=300000, stack=1003, elapsed=5.29s, progress_done=1960
... DFS nodes=400000, stack=1019, elapsed=7.05s, progress_done=1969
... DFS nodes=500000, stack=929, elapsed=8.79s, progress_done=1814
... DFS nodes=600000, stack=887, elapsed=10.70s, progress_done=1762
... DFS nodes=650000, stack=971, elapsed=11.58s, progress_done=1910
DFS finished. result: b'moectf{I5_1t_Stream0rBlock.?}' nodes_used: 667623
Found by DFS, skipping random trials.

=== FOUND by DFS ===
 b'moectf{I5_1t_Stream0rBlock.?}'

'''

sandtea姐姐的fufu

背包问题 让GPT老师梭了 就不放exp了()

半^3部电台

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
from random import choice
from Crypto.Util.number import bytes_to_long, long_to_bytes

with open('flag.txt', 'r') as file:
    flag = file.read()

class MACHINE:
    def __init__(self):
        self.alphabet = 'abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ ,.!?()\n'

        self.IP = [58, 50, 42, 34, 26, 18, 10, 2,
              60, 52, 44, 36, 28, 20, 12, 4,
              62, 54, 46, 38, 30, 22, 14, 6,
              64, 56, 48, 40, 32, 24, 16, 8,
              57, 49, 41, 33, 25, 17, 9, 1,
              59, 51, 43, 35, 27, 19, 11, 3,
              61, 53, 45, 37, 29, 21, 13, 5,
              63, 55, 47, 39, 31, 23, 15, 7
              ]

        self.IP_inv = [self.IP.index(i) + 1 for i in range(1, 65)]

        self.S1 = [14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7,
              0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8,
              4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0,
              15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13
              ]
        self.S2 = [15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10,
              3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5,
              0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15,
              13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9
              ]
        self.S3 = [10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8,
              13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1,
              13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7,
              1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12
              ]
        self.S4 = [7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15,
              13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9,
              10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4,
              3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14
              ]
        self.S5 = [2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9,
              14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6,
              4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14,
              11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3
              ]
        self.S6 = [12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11,
              10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8,
              9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6,
              4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13
              ]
        self.S7 = [4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1,
              13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6,
              1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2,
              6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12
              ]
        self.S8 = [13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7,
              1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2,
              7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8,
              2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11
              ]
        self.S = [self.S1, self.S2, self.S3, self.S4, self.S5, self.S6, self.S7, self.S8]

        self.E = [32, 1, 2, 3, 4, 5, 4, 5,
             6, 7, 8, 9, 8, 9, 10, 11,
             12, 13, 12, 13, 14, 15, 16, 17,
             16, 17, 18, 19, 20, 21, 20, 21,
             22, 23, 24, 25, 24, 25, 26, 27,
             28, 29, 28, 29, 30, 31, 32, 1
             ]

        self.P = [16, 7, 20, 21, 29, 12, 28, 17,
             1, 15, 23, 26, 5, 18, 31, 10,
             2, 8, 24, 14, 32, 27, 3, 9,
             19, 13, 30, 6, 22, 11, 4, 25
             ]

        self.PC_1 = [57, 49, 41, 33, 25, 17, 9,
                1, 58, 50, 42, 34, 26, 18,
                10, 2, 59, 51, 43, 35, 27,
                19, 11, 3, 60, 52, 44, 36,
                63, 55, 47, 39, 31, 23, 15,
                7, 62, 54, 46, 38, 30, 22,
                14, 6, 61, 53, 45, 37, 29,
                21, 13, 5, 28, 20, 12, 4
                ]

        self.PC_2 = [14, 17, 11, 24, 1, 5, 3, 28,
                15, 6, 21, 10, 23, 19, 12, 4,
                26, 8, 16, 7, 27, 20, 13, 2,
                41, 52, 31, 37, 47, 55, 30, 40,
                51, 45, 33, 48, 44, 49, 39, 56,
                34, 53, 46, 42, 50, 36, 29, 32
                ]

        self.shift_num = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]

        self.key = ''.join(choice(self.alphabet) for _ in range(8))
        self.subkey = self.generate_key(self.key.encode())

    def generate_key(self, ori_key):
        key = bin(bytes_to_long(ori_key))[2:].zfill(64)
        subkeys = []
        temp = [key[i - 1] for i in self.PC_1]
        for i in self.shift_num:
            temp[:28] = temp[:28][i:] + temp[:28][:i]
            temp[28:] = temp[28:][i:] + temp[28:][:i]
            subkeys.append(''.join(temp[j - 1] for j in self.PC_2))
        return subkeys

    def encrypt(self, text):
        if isinstance(text, str):
            text = text.encode()
        bin_flag = ''.join([bin(byte)[2:].zfill(8) for byte in text])

        padded_len = (64 - (len(bin_flag) % 64)) % 64
        padded_flag = bin_flag + '0' * padded_len

        cate_text = [padded_flag[i * 64:(i + 1) * 64] for i in range(0, len(padded_flag) // 64)]

        encrypted_text = ''
        for text in cate_text:
            t = ''.join(text[i - 1] for i in self.IP)
            L, R = t[:32], t[32:]

            for cnt in range(2):
                R_temp = R
                k = self.subkey[cnt]
                R_expanded = ''.join(R[i - 1] for i in self.E)
                R_xor = [str(int(R_expanded[i]) ^ int(k[i])) for i in range(48)]
                R_groups = [R_xor[i:i + 6] for i in range(0, 48, 6)]
                res = ''
                for i in range(8):
                    row = int(R_groups[i][0] + R_groups[i][5], base=2)
                    col = int(''.join(R_groups[i][1:5]), base=2)
                    int_res = self.S[i][16 * row + col]
                    res += bin(int_res)[2:].zfill(4)

                res_p = ''.join(res[i - 1] for i in self.P)
                new_R = ''.join(str(int(res_p[i]) ^ int(L[i])) for i in range(32))
                R = new_R
                L = R_temp

            t = R + L
            t = ''.join(t[i - 1] for i in self.IP_inv)
            encrypted_text += t

        encrypted_bytes = b''
        for i in range(0, len(encrypted_text), 8):
            byte = int(encrypted_text[i:i + 8], 2)
            encrypted_bytes += bytes([byte])
        encrypted_text = encrypted_bytes
        return encrypted_text

machine = MACHINE()
text = ''.join(choice('abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ ,.!?()\n') for _ in range(80))
en_text = machine.encrypt(text)
en_flag = machine.encrypt(flag)

print("Encrypted flag:", bytes_to_long(en_flag))
print("Random text:", bytes_to_long(text.encode()))
print("Encrypted random text:", bytes_to_long(en_text))

# Random text: 1733571697283962509488226713108269753699322498714010326656310076489877844089729148788129403124099930593602491145395337324365415309638864335256126266980930992016878248102013062728229825856295255
# Encrypted random text: 3578059052586522474100389050030320588160089073371878413925896715373042626307922378489203525965322427489129100605094275877241918595390796602423805072859665451626477779012814084741966341775758398

一个对称问题，类似魔改的DES加密Fesitel网格，块加密的思路为

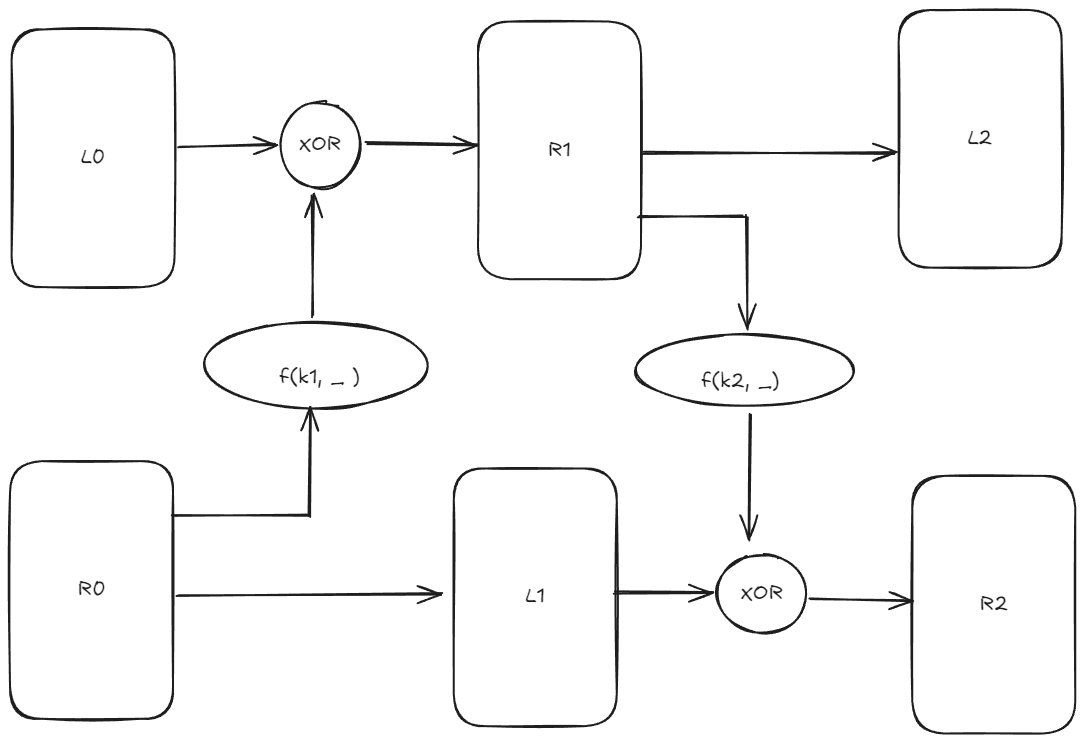
block

我们能得到

DES的轮函数是 是一个的映射，是一个的原地置换，我们已知,可以得到

在DES中我们的操作是一种对应盒中的查表操作即 也就是对于我们这里的的延展和位的密钥异或后，我们可以考虑把它分为组，每组位，对应到盒中进行一个查表，得到最终的输出空间

对于已知的，我们完全可以由已知的明文块计算出可能的,它的可能性最多有种，对于多个明文我们取交集即可找到这里的密钥,恢复我们的密钥后就正常解密即可

这里的关键点就是二轮Fesitel网络的安全性太低 我们可以通过简单的推导从已知的明文块密文块泄露大部分有关密钥的信息

同样的，exp by GPT5老师

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
# We'll reconstruct the 2-round DES-like cipher, recover K1 and K2 from the provided
# known plaintext/ciphertext pair, then decrypt the uploaded encrypted_flag.
# The user supplied two big integers for Random text and Encrypted random text in the chat.
# The encrypted_flag big integer was uploaded to /mnt/data/encrypted_flag.txt.

from pathlib import Path

# ---- Tables copied from the user's cipher (DES tables) ----
IP = [58, 50, 42, 34, 26, 18, 10, 2,
      60, 52, 44, 36, 28, 20, 12, 4,
      62, 54, 46, 38, 30, 22, 14, 6,
      64, 56, 48, 40, 32, 24, 16, 8,
      57, 49, 41, 33, 25, 17, 9, 1,
      59, 51, 43, 35, 27, 19, 11, 3,
      61, 53, 45, 37, 29, 21, 13, 5,
      63, 55, 47, 39, 31, 23, 15, 7
      ]

IP_inv = [IP.index(i) + 1 for i in range(1, 65)]

S1 = [14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7,
      0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8,
      4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0,
      15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13
      ]
S2 = [15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10,
      3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5,
      0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15,
      13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9
      ]
S3 = [10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8,
      13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1,
      13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7,
      1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12
      ]
S4 = [7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15,
      13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9,
      10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4,
      3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14
      ]
S5 = [2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9,
      14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6,
      4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14,
      11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3
      ]
S6 = [12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11,
      10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8,
      9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6,
      4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13
      ]
S7 = [4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1,
      13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6,
      1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2,
      6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12
      ]
S8 = [13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7,
      1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2,
      7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8,
      2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11
      ]
S = [S1, S2, S3, S4, S5, S6, S7, S8]

E = [32, 1, 2, 3, 4, 5, 4, 5,
     6, 7, 8, 9, 8, 9, 10, 11,
     12, 13, 12, 13, 14, 15, 16, 17,
     16, 17, 18, 19, 20, 21, 20, 21,
     22, 23, 24, 25, 24, 25, 26, 27,
     28, 29, 28, 29, 30, 31, 32, 1
     ]

P = [16, 7, 20, 21, 29, 12, 28, 17,
     1, 15, 23, 26, 5, 18, 31, 10,
     2, 8, 24, 14, 32, 27, 3, 9,
     19, 13, 30, 6, 22, 11, 4, 25
     ]

# ---- Helpers ----
def bbits(x, n): 
    return bin(x)[2:].zfill(n)

def perm(bits, T): 
    return ''.join(bits[i-1] for i in T)

def xor(a, b): 
    return ''.join('01'[a[i] != b[i]] for i in range(len(a)))

# P inverse
P_inv = [0]*32
for i, p in enumerate(P):
    P_inv[p-1] = i+1

def sbox_preimages(si, out4_bits):
    want = int(out4_bits, 2)
    outs = []
    Sbox = S[si]
    for x in range(64):
        row = ((x >> 5) & 1) * 2 + (x & 1)
        col = (x >> 1) & 0b1111
        if Sbox[16*row + col] == want:
            outs.append(bbits(x, 6))
    return outs

def to_blocks_from_int(n):
    bs = n.to_bytes((n.bit_length()+7)//8, 'big')
    if len(bs) % 8 != 0:
        bs = b'\x00'*(8 - (len(bs) % 8)) + bs
    return [bs[i:i+8] for i in range(0, len(bs), 8)]

def bits_of_bytes(B):
    return ''.join(bbits(x, 8) for x in B)

def recover_subkeys(plain_blocks, cipher_blocks):
    cand1 = [None]*8
    cand2 = [None]*8
    for pb, cb in zip(plain_blocks, cipher_blocks):
        Pbits = bits_of_bytes(pb)
        Cbits = bits_of_bytes(cb)
        L0R0 = perm(Pbits, IP);  L0, R0 = L0R0[:32], L0R0[32:]
        R2L2 = perm(Cbits, IP);  R2, L2 = R2L2[:32], R2L2[32:]
        # Targets
        T1 = xor(L0, L2)  # = f(R0, K1)
        T2 = xor(R0, R2)  # = f(L2, K2)
        Sout1 = perm(T1, P_inv)
        Sout2 = perm(T2, P_inv)
        eR0 = perm(R0, E)
        eL2 = perm(L2, E)
        for i in range(8):
            need1 = Sout1[4*i:4*i+4]
            need2 = Sout2[4*i:4*i+4]
            k1set = {xor(eR0[6*i:6*i+6], x) for x in sbox_preimages(i, need1)}
            k2set = {xor(eL2[6*i:6*i+6], x) for x in sbox_preimages(i, need2)}
            cand1[i] = k1set if cand1[i] is None else (cand1[i] & k1set)
            cand2[i] = k2set if cand2[i] is None else (cand2[i] & k2set)
    # Choose unique candidates (should be unique with enough blocks)
    K1 = ''.join(next(iter(s)) for s in cand1)
    K2 = ''.join(next(iter(s)) for s in cand2)
    return K1, K2

def des2_process(block_bytes, Klist):  # Klist: [K1, K2] or [K2, K1] for decrypt
    bits = bits_of_bytes(block_bytes)
    t = perm(bits, IP)
    L, R = t[:32], t[32:]
    for k in Klist:
        eR = perm(R, E)
        x = xor(eR, k)
        out = ''
        for i in range(8):
            xi = x[6*i:6*i+6]
            row = int(xi[0] + xi[5], 2)
            col = int(xi[1:5], 2)
            out += bbits(S[i][16*row + col], 4)
        f = perm(out, P)
        L, R = R, xor(L, f)
    t = R + L
    outbits = perm(t, IP_inv)
    return int(outbits, 2).to_bytes(8, 'big')

def des2_decrypt_bytes(ct_bytes, K1, K2):
    out = b''
    for i in range(0, len(ct_bytes), 8):
        out += des2_process(ct_bytes[i:i+8], [K2, K1])  # reverse order to decrypt
    # Zero-bit padding → at byte-level becomes zero bytes at end
    return out.rstrip(b'\x00')

# ---- Use the user's provided big integers for known pair ----
random_plain_int = int("1733571697283962509488226713108269753699322498714010326656310076489877844089729148788129403124099930593602491145395337324365415309638864335256126266980930992016878248102013062728229825856295255")
random_cipher_int = int("3578059052586522474100389050030320588160089073371878413925896715373042626307922378489203525965322427489129100605094275877241918595390796602423805072859665451626477779012814084741966341775758398")

plain_blocks = to_blocks_from_int(random_plain_int)
cipher_blocks = to_blocks_from_int(random_cipher_int)

# Sanity: lengths should match
assert len(plain_blocks) == len(cipher_blocks), (len(plain_blocks), len(cipher_blocks))

# Recover subkeys
K1, K2 = recover_subkeys(plain_blocks, cipher_blocks)

# ---- Load encrypted_flag (decimal integer) from the uploaded file ----
enc_flag_path = Path("encrypted_flag.txt")
enc_str = enc_flag_path.read_text().strip()
# It might be a bare decimal or include label—strip non-digits except leading minus (shouldn't be negative)
import re
m = re.search(r'(\d+)', enc_str)
if not m:
    raise ValueError("Could not find a decimal integer in /mnt/data/encrypted_flag.txt")
encrypted_flag_int = int(m.group(1))

# Convert to bytes (pad to 8-byte multiple)
ct = encrypted_flag_int.to_bytes((encrypted_flag_int.bit_length()+7)//8, 'big')
if len(ct) % 8 != 0:
    ct = b'\x00' * (8 - len(ct) % 8) + ct

# Decrypt
flag_bytes = des2_decrypt_bytes(ct, K1, K2)
try:
    flag_text = flag_bytes.decode()
except UnicodeDecodeError:
    flag_text = flag_bytes.decode('utf-8', errors='replace')

print("Recovered K1 (48 bits):", K1)
print("Recovered K2 (48 bits):", K2)
print("\nDecrypted flag:\n", flag_text)

'''
Recovered K1 (48 bits): 111000001011111001000100111111010100111010100001
Recovered K2 (48 bits): 101000000011010001110110001100111111101001100100

Decrypted flag:
 Dear Alice,

I hope this message finds you wel1. I鈥檓 writing to tell you that I鈥檝e been participating in Moectf recently ,
it鈥檚 a cybersecurity competition designed for students like you and me. The contest offers various tracks
such as Web, Pwn, and morE.Based on my interest5, I chose the Crypto track.
Since you鈥檝e been my long-time partner in cryptology, I鈥檓 sure you understand how much I wish our communication
could be free from the threats of cryptographic attackS. Every time we try to connect over the internet, it feels
like there鈥檚 someone trying to steal our informatioN. How frustrating!
That鈥檚 why I believe we should learn more about cryptography to better protect ourselves!. If you agree with my idea,
please include the flag hidden in this letter in your next replyy. If you鈥檙e not sure what it is, try connecting all
the characters that come before dots in this letter into one lin3.

Looking forward to hearing from you!
Yours,
Bob
'''

简单分析输出后得到flagmoectf{1eEkSN!y3}

Ez_wiener

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from Crypto.Util.number import*
from secret import flag

p=getPrime(512)
q=getPrime(512)
m=bytes_to_long(flag)
n=p*q
phi_n=(p-1)*(q-1)
while True:
    nbits=1024
    d = getPrime(nbits // 5)
    if (GCD(d, phi_n) == 1 and 30 * pow(d, 4) < n):

        break
e = pow(d,-1,phi_n)

c=pow(m,e,n)

print ("n=",n)
print ("e=",e)
print ("c=",c)

基于连分数的Wiener攻击，思路如下

当 由于我们有

即 我们引入Legendre's theorem

如果存在 满足

我们称是的一个有理近似

故这里，我们想想，在RSA中 而我们往往已知，能否说就近似,是的一个有理近似呢？

我们来算一下

而 故 我们又知道必有 是能计算的前提

所以 推出误差限为 且要满足 大概就是卡这个

思路明确了，在这种情况下我们计算,就能得到一个的有理近似，然后对它连分数展开

得到若干组可能的，还是因为 那么 挨个验证就能找出我们需要的了

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
from Crypto.Util.number import *

n= 
e= 
c= 

def wienerAttack(N, e):
    """
    维纳攻击

    `Parameters`:
        N - p * q\\
        e - public key
    
    `Returns`:
        p, q, d
    """
    cf = continued_fraction(e / N)
    convers = cf.convergents()
    for pkd in convers:
        # possible k, d
        pk, pd = pkd.as_integer_ratio()
        if pk == 0:
            continue
        
        # verify
        if (e * pd - 1) % pk != 0:
            continue
        
        # possible phi
        pphi = (e * pd - 1) // pk
        p = var('p', domain=ZZ)
        roots = solve(p ** 2 + (pphi - N - 1) * p + N, p)
        if len(roots) == 2:
            # possible p, q
            pp, pq = roots
            if pp * pq == N:
                return pp, pq, pd
    raise ValueError('Could not factor N!')

pp,pq,pd = wienerAttack(n,e)
print(long_to_bytes(pow(c,pd,n)))
# b'moectf{Ez_W1NNer_@AtT@CK!||}'

prime-in-prime

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
from Crypto.Util.number import long_to_bytes, bytes_to_long, getPrime
import random, gmpy2
from secret import flag

class RSAEncryptor:
    def __init__(self):
        self.g = self.a = self.b = 0
        self.e = 65537
        self.factorGen()
        self.product()

    def factorGen(self):
        while True:
            self.g = getPrime(256)
            while not gmpy2.is_prime(2*self.g*self.a+1):
                self.a = random.randint(2**255, 2**256)
            while not gmpy2.is_prime(2*self.g*self.b+1):
                self.b = random.randint(2**255, 2**256)
            self.h = 2*self.g*self.a*self.b+self.a+self.b
            if gmpy2.is_prime(self.h):
                self.N = 2*self.h*self.g+1
                print(len(bin(self.N)))
                return

    def encrypt(self, msg):
        return pow(msg, self.e, self.N)


    def product(self):
        self.flag =bytes_to_long(flag)
        self.enc = self.encrypt(self.flag)
        self.show()
        print(f'enc={self.enc}')

    def show(self):
        print(f"N={self.N}")
        print(f"e={self.e}")
        print(f"g={self.g}")


RSAEncryptor()


我们有 已知 不难得到

我们考虑 同时 可以搜索，应该不大的

如果有 说明找到了

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
from Crypto.Util.number import *
N=
e=
g=
enc=
assert (N-1) % (2*g) == 0
h = (N-1)//(2*g)
S = h % g

for k in range(2,100):
    sumAB = S+k*g
    if (h-sumAB) % g == 0:
        timesAB = (h-sumAB) // (2*g)
        print(f"found k = {k}")
        print(f"found a + b :{sumAB}")
        print(f"found a * b :{timesAB}")
        break

var('x')
eq = x^2 - sumAB*x + timesAB == 0
solve(eq,x)

a = 101126341585289743784212995522825940940572948851643611527478964050349909608133
b = 98232570102966693249299409844742571202213308729052846054661370108045547681410
p = 2*g*a+1
q = 2*g*b+1
phi = (p-1)*(q-1)
print(phi)
d = inverse_mod(e,phi)
print(d)
print(pow(enc,d,N))
print(long_to_bytes(pow(enc,d,N)))

# b'moectf{Ju57_@_5YmP1e_C0mm0n_Pr1me#!}'

貌似是RSA Common Prime Attack

ez_lattice

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
from random import randrange
from Crypto.Util.number import getPrime, bytes_to_long
from secret import flag
assert len(flag) % 5 == 0

block_size = len(flag) // 5
m_blocks = [bytes_to_long(flag[i*block_size:(i+1)*block_size])for i in range(5)]
p = getPrime(128)

def make_mask(n, p):
    from sage.all import identity_matrix, det
    upper = identity_matrix(n)
    low   = identity_matrix(n)
    for i in range(n-1):
        for j in range(i+1, n):
            upper[i, j] = randrange(1, p)
            low[j, i]   = randrange(1, p)
    result = upper * low
    assert det(result) == 1
    return result

def matrix_to_list(mat):
    return [list(row) for row in mat]

Noise = [[randrange(1, p) for _ in range(5)] for _ in range(4)]
Noise.append(m_blocks)

M = matrix(Noise)
A = make_mask(5, p)
C = A * M

print(f"p={p}")
print(f"C={matrix_to_list(C)}")

矩阵运算的左乘不会影响格基的线性关系 我们的flag总是保持是最优的这个线性组合 ，题目相当于对flag矩阵进行线性组合得到C，而我们的基却直接是直接考虑对做格基归约即可

exp

1
2
3
4
5
6
7
8
9
10
p=
C=
C = Matrix(ZZ,C)
C = C.LLL()
v = C[0]
flag = b''
for i in v:
    flag += long_to_bytes(abs(i))
print(flag)
# b'moectf{h0w_P0werfu1_7he_latt1ce_1s}'

happyRSA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from Crypto.Util.number import getPrime, bytes_to_long
from random import randint
from sympy import totient
from secret import flag

def power_tower_mod(a, k, m):  # a↑↑k mod m
    if k == 1:
        return a % m
    exp = power_tower_mod(a, k - 1, totient(m))
    return pow(a, int(exp), int(m))


p = getPrime(512)
q = getPrime(512)
r = 123456
n = p * q
e = 65537
n_phi= p+q-1
x=power_tower_mod(n_phi + 1, r, pow(n_phi, 3))
m = bytes_to_long(flag)
c = pow(m, e, n)

print(f"n = {n}")
print(f"e = {e}")
print(f"c = {c}")
print(f"x = {x}")

幂塔是123456层深

尝试有 我们视为一个二项式的形式，也就是

其中我们的是

我们先考虑对(1)来展开，超过3次幂的都会被约去，也就是 我们接下来想知道模,的值 方便我们把这里的模往下去换

显然有 那么就有 然后对于大于2的,也不难得到

我们又已经有 也就是 带入即可得 从我们已有的信息 有 带入上式 大于3的次方消掉 就得到了 然后解，求，exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from Crypto.Util.number import *
from random import randint
from sympy import totient

n = 
e = 65537
c = 
x = 
# var('s')
# eq = s^2+s + 1 - x 
# res = solve(eq,s)
# print(res)
ss = 
s = ss+1
var("p")
eq = p + n / p - s
res = solve(eq, p)
# print(res)
# pp = int(res[0])
pp = 
assert n % pp == 0
qq = n // pp
pphi = (pp-1)*(qq-1)
d = inverse_mod(e,pphi)
print(long_to_bytes(pow(c,d,n)))

# b'moectf{rsa_and_s7h_e1se}'

ezhalf_gcd

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from Crypto.Util.number import bytes_to_long, getStrongPrime
from secret import flag


e = 11
p = getStrongPrime(1024)
q = getStrongPrime(1024)
n = p * q
phi = (p - 1) * (q - 1)
d = pow(e, -1, phi)
enc_d = pow(d, e, n)
enc_phi = pow(phi, e, n)
enc_flag = pow(bytes_to_long(flag), e, n)
print(f"{e=}")
print(f"{n = }")
print(f"{enc_d = }")
print(f"{enc_phi = }")
print(f"{enc_flag = }")

给了你

考虑恢复出我们的

我们已知 也就是说，之间存在线性关系，我们不妨设 那题目就变成了 这里有,直接爆破，发现取的时候都只返回了一个常数项，带入发现解不出flag，取的时候给我们返回了一个一次多项式，sage解有点麻烦 ，手动提系数出来处理即可，exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
from Crypto.Util.number import *
e=11
n = 31166099657280475125475535365831782783093875463247358362475188588947278779261659087382153841735341294644470135658242563894811427195085499234687959821014213884097144683916979145688501653937652132196507641706592058541461494851978378234097501450088696202067780458185699118745693112795064523774316076900622924515043087514299819363383005261432426124907190050031873969718731577577610423430342011833399812571330259167141343053584093492407110726050289284883569075898031613703838488237576756303655189545592872431914967027530453720947545137077577544615857606624432667091058064432254815560483584621525418467954592836937243988243
enc_d = 13808910452602719582082356538103809869422886228259509560372242093772427733416618401205696740074353028623820317050192627491660359558892392153999532272857339481298482802886251848703046960504786528793589170539584003383632027476914361574273144291330585735179166690513545471901763697269194228467287645573188775899890375853801796593582850975578804671547453457528686518397397234277841944184055117669277697362945463508844599947716337314398521363079749738943908860398843430518505690528296941997988869732759053587554475692300841912141199296010163641185664377742397777941968394746150611710777000625916609542525700860321528867212
enc_phi = 7712799451523923934297438340493818709638100911475880659269081521797448094000671886662453371669377561442768781648787281763679814952312810588749220640616349121013802986627369725105748412428708271146640375251603852154891826036699121824706508396445679193881511426962350499448921650925902083009038656420224517990418144263810608916613943703387804258988710100695100014625921151006914635066745373266932452264209581055597451243351753611834270245107587926127995770837997657200564139159783438755362906511732933456755615781562673235575025697927723044975521898510169824612319133648292886516647301360818651593931313229819219102145
enc_flag = 894510730103475572849584456948777906177928458037601077973815297094718207962800841050676989919558783959100151883021776468599378605624814726543232609670826195546342526501910728018180564277901156145145431115589678554941920392777979439329210254339330200637295639957614541733453280727879958971862238162005775966684182859139832583501267115086918765938983728386252082360729694525611252282765144977858082339098241367689924035089953114271269967974794791094625994785638389602317004891381734713155429498571328372671258967340771255624802290579938944569672935599910907961053536945947262426210286500553262856689698523083914877686

def HGCD(a, b):
    if 2 * b.degree() <= a.degree() or a.degree() == 1:
        return 1, 0, 0, 1
    m = a.degree() // 2
    a_top, a_bot = a.quo_rem(x ^ m)
    b_top, b_bot = b.quo_rem(x ^ m)
    R00, R01, R10, R11 = HGCD(a_top, b_top)
    c = R00 * a + R01 * b
    d = R10 * a + R11 * b
    q, e = c.quo_rem(d)
    d_top, d_bot = d.quo_rem(x ^ (m // 2))
    e_top, e_bot = e.quo_rem(x ^ (m // 2))
    S00, S01, S10, S11 = HGCD(d_top, e_top)
    RET00 = S01 * R00 + (S00 - q * S01) * R10
    RET01 = S01 * R01 + (S00 - q * S01) * R11
    RET10 = S11 * R00 + (S10 - q * S11) * R10
    RET11 = S11 * R01 + (S10 - q * S11) * R11
    return RET00, RET01, RET10, RET11
 
def related_message_attack(a, b):
    q, r = a.quo_rem(b)
    if r == 0:
        return b
    R00, R01, R10, R11 = HGCD(a, b)
    c = R00 * a + R01 * b
    d = R10 * a + R11 * b
    if d == 0:
        return c.monic()
    q, r = c.quo_rem(d)
    if r == 0:
        return d
    return related_message_attack(d, r)

R.<x> = Zmod(n)[]


f1 = x^e - enc_d

for k in range(0, e):
    
    f2 = (e * x - 1)^e - k^e * enc_phi
    poly = (related_message_attack(f1,f2))
    # roots = poly.roots(multiplicities=False)

    print(poly)
# 13956969191637195871632957505406117751565360403440829727249072761352047425739750866240599441725739309449282190348085360109677584507525554127026445196148893160857286022203801997873156811960571737271597472086993749971283966198697191943628862781066725335706690253538900770669084526246573003464456817905257894602490888900824860753149136591999728629106864099281400347411046856634802687971218504308172469580264497048520451583896989424545232463140527591539153615957817302334587761071546151380508318892302985208301605902883263311183702458763989755391843198670020891760809561155674454979493217081297358303315754142647867287413*x + 17608846521747499227247968154910171731843801156227555409194280778664071883264366214940238190095425116113057138491957289339384506579980194769451841153928528442505720494339582748962879927154787429060456888699871619817359888932353097693698140571527638555084889587814391101653933403674692802280381912990231017047722784101787449714956539028428195425358869511831219379267775628816285643329918029273198098018020166399500224247055896233457476227184648878532488798022601672987527850189642016707592877060843958894268793661605698870282835092803537046968215660983366498922624712685432673765041272654998087422047424791161022662127

解方程

1
2
3
4
5
6
7
8
9
k1 = 13956969191637195871632957505406117751565360403440829727249072761352047425739750866240599441725739309449282190348085360109677584507525554127026445196148893160857286022203801997873156811960571737271597472086993749971283966198697191943628862781066725335706690253538900770669084526246573003464456817905257894602490888900824860753149136591999728629106864099281400347411046856634802687971218504308172469580264497048520451583896989424545232463140527591539153615957817302334587761071546151380508318892302985208301605902883263311183702458763989755391843198670020891760809561155674454979493217081297358303315754142647867287413
k2 = 17608846521747499227247968154910171731843801156227555409194280778664071883264366214940238190095425116113057138491957289339384506579980194769451841153928528442505720494339582748962879927154787429060456888699871619817359888932353097693698140571527638555084889587814391101653933403674692802280381912990231017047722784101787449714956539028428195425358869511831219379267775628816285643329918029273198098018020166399500224247055896233457476227184648878532488798022601672987527850189642016707592877060843958894268793661605698870282835092803537046968215660983366498922624712685432673765041272654998087422047424791161022662127
inv = inverse_mod(k1,n)
# print(inv)
pd = (-k2 * inv) % n
print(pd)
m = pow(enc_flag,pd,n)
print(long_to_bytes(m))
# b'moectf{N0w_y0u_kn0w_h0w_t0_g3t_th1s_fl@G__!!!!!!!!!!}'

神秘数字太多了

转化为带的幂式求解即可

即 没什么区别

1
2
3
4
5
6
7
8
9
10
11
p = 10000000000099
a = 114514
t = a*9 + 1
b = 10
F = GF(p)
b = F(b)
t = F(t)
N = discrete_log(t,b)
flag = "moectf{" + str(N) + "}"
print(flag)
# moectf{7718260004383}

wiener++

三元ExtendWienerAttack 直接梭别的师傅的板子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
E = 
c = 
n = 
e1,e2,e3 = E[0],E[1],E[2]
L = matrix(ZZ, [
    [1, -n, 0, n**2, 0, 0, 0, -n**3],
    [0, e1, -e1, -n * e1, -e1, 0, n * e1, n**2 * e1],
    [0, 0, e2, -n * e2, 0, n * e2, 0, n**2 * e2],
    [0, 0, 0, e1 * e2, 0, -e1 * e2, -e1 * e2, -n * e1 * e2],
    [0, 0, 0, 0, e3, -n * e3, -n * e3, n**2 * e3],
    [0, 0, 0, 0, 0, e1 * e3, 0, -n * e1 * e3],
    [0, 0, 0, 0, 0, 0, e2 * e3, -n * e2 * e3],
    [0, 0, 0, 0, 0, 0, 0, e1 * e2 * e3]
])
alpha = 600 / 2048
# alpha = 2 / 5
D = diagonal_matrix(ZZ, [floor(pow(n, 3 / 2)), n, floor(pow(n, alpha + 3/2)), floor(pow(n, 1/2)), floor(pow(n, alpha + 3/2)), floor(pow(n, alpha + 1)), floor(pow(n, alpha + 1)), 1])
M = L * D
B = M.LLL()
b = vector(ZZ, B[0])
A = b * M^(-1)
phi = floor(A[1] / A[0] * e1)

d = inverse_mod(0x10001, phi)
m = pow(c, d, n)
flag = long_to_bytes(int(m))
print(flag)
# b'moectf{W1N4er_A@tT@CkRR-R@4ENggeEE|!}'

湾区杯2025出过一道非常诡异的的二元EWA 还没看到预期解（草

ledengre_revenge

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
from Crypto.Util.number import *
from Crypto.Cipher import AES
import gmpy2
import random
from secrets import flag

p=251
e=65537

def function(x,p):
    y=0
    if x>=p:
        y=x
    elif pow(x,(p-1)//2,p)==1:
        y=pow(x,2,p)
    else:
        y=pow(x,3,p)
    return y

def matrix_to_str(matrix):
    b = bytes(sum([[matrix[row][col] for col in range(4)] for row in range(4)], []))
    return b.rstrip(b'\0')


def str_to_matrix(s):
    matrix = [[function(s[row + 4*col],p) for row in range(4)] for col in range(4)]
    return matrix

a=[[random.choice([227,233,239,251]) for row in range(4)] for col in range(4)]
p_=getPrime(256)

text_=[[pow(bytes_to_long(flag[(row+col*4)*2:(row+col*4)*2+2]),-2,p_)+1 for row in range(4)] for col in range(4)]
key = 0
for row in range(4):
    for col in range(4):
        key*=2
        key+=(pow(text_[row][col],(p_-1)//2,p_)+1)%p_//2

assert len(flag)==32
assert p_ == 71583805456773770888820224577418671344500223401233301642692926000191389937709
assert pow(key,2*e,p_) == 1679283667939124174051653611794421444808492935736643969239278575726980681302


text_=[flag[:16],flag[16:]]
cipher = AES.new(long_to_bytes(key<<107), AES.MODE_ECB)
for t in range(2):
    lis=[[0 for row in range(4)] for col in range(4)]
    for i in range(10):
        enc = cipher.encrypt(text_[t])
        matrix = str_to_matrix(enc)
        for row in range(4):
            for col in range(4):
                lis[row][col]=lis[row][col] << 1
                if matrix[row][col]>a[row][col]//2:
                    lis[row][col]+=1
        matrix = [[function(matrix[col][row],a[col][row]) for row in range(4)] for col in range(4)]
        text_[t] = matrix_to_str(matrix)
    print(f"lis{t}={lis}")

text=pow(bytes_to_long(text_[0]+text_[1]),2,p_)
print(f"text={text}")
print(f"a={a}")

'''
lis0=[[341, 710, 523, 1016], [636, 366, 441, 790], [637, 347, 728, 426], [150, 184, 421, 733]]
lis1=[[133, 301, 251, 543], [444, 996, 507, 1005], [18, 902, 379, 878], [235, 448, 836, 263]]
text=26588763961966808496088145486940545448967891102453278501457496293530671899568
a=[[239, 239, 251, 239], [233, 227, 233, 251], [251, 239, 251, 233], [233, 227, 251, 233]]
'''

系统比较繁，整理一下就是

part1.

给出32字节的flag，两个字节两个字节的切片，切出16块放到一个的矩阵中，对每个矩阵中的数，计算它对p_的勒让德符号，如果是二次剩余，代表1，不是二次剩余，代表0，最终拼起来得到一个16位的key，由这个key构造AES加密器，同时还给出了 part2.

把flag拆成左右各16字节两个块，作为text数组的初始值，

随后的操作进行10轮

​ 对块中16字节进行加密后得到enc密文，拆成16份放到4*4矩阵中，构造出matrix, 每份1字节，同时我们定义一个标记矩阵lis用来记录我们比较的结果，

​ 对于加密矩阵matrix中的每一个值，和给定的矩阵a进行一个比较，如果满足给定的大小关系，我们就给lis标记矩阵的这一个元素的这一位是1，否则是0

​ 最后对每个元素，我们丢入function,构造出一个处理后的矩阵matrix，

最后给你的是两轮比较的结果lis 以及初始的a矩阵 两端text的计算处理结果

信息很多 很杂 我们来分析一下我们有什么

  • e

  • p ,也就是function

  • p_

  • ，考虑试试离散对数？

  • flag的长度

  • 用于比较的标准矩阵a

  • 两轮比较结果lis

  • 密文处理结果text

我们先尝试能不能通过离散对数求出,p_ - 1很光滑，还已知key的范围是，即解，exp

1
2
3
4
5
6
7
8
9
10
11
12
p_ = 71583805456773770888820224577418671344500223401233301642692926000191389937709
b = 1679283667939124174051653611794421444808492935736643969239278575726980681302
e = 65537
P = GF(p_)
b = P(b)
roots = b.nth_root(n, all=True)
for i in roots:
    if i < 65536:
        key = i
assert pow(key,2*e,p_) == b
print(key)
# 60679

求出来key后 我们有两点突破，首先是AES加密器相当于白盒了，其次我们会看key的生成过程，看看能不能推导出原本flag的某些信息

我们看向key的生成过程

1
2
3
4
5
6
text_=[[pow(bytes_to_long(flag[(row+col*4)*2:(row+col*4)*2+2]),-2,p_)+1 for row in range(4)] for col in range(4)]
key = 0
for row in range(4):
    for col in range(4):
        key*=2
        key+=(pow(text_[row][col],(p_-1)//2,p_)+1)%p_//2

把flag拆成16个块，每个块2字节，对于每两个字节的块 ，我们可以去算它的text，也就是

1
2
f_i = bytes_to_long(flag_block_i)
text_i = pow(f_i,-2,p_) + 1

然后key在这一位的比特说明了text_i对p_是否是二次剩余，我们很难逆向求flag 但是保留了验证flag的一个思路

随后我们分析后面的比较以及矩阵构造的过程，key已知 ,而且注意到这里的AES是ECB模式，也就是说flag的块与块之间的加密是互不干扰的，加上我们已知了

flag第一个块是moectf{?????????,此时爆破就具备一定可行性了，接着往下看，lis实际就是flag放进去验证的过程 ，但是实际中我们组合的时候满足条件的二次剩余&二次非剩余的取值还是太多 不能爆破

而且上述做法实际上没有用到题目给定的text ，于是还是尝试从终态的text结构逆向来求解这个问题

最关键的点在于函数function是否可逆？

题目给我们的素数p=251实际上满足 因此对于function,这里计算的结果对于任何输入的都是一一对应的，也就是双射

当取到剩下的227 239 233的时候，也都满足 此时对于取立方的情况，是一个双射，而且我们还有一个lis数组用来限定我们，也就是说你逆向这个函数，只需要在的范围内枚举然后带进去算即可，基本上是一一对应的，我们实现了function的逆向 实际上也就实现了系统的逆向，下面分阶段编写exp

首先根据最终的text还原我们末态的text状态

1
2
3
4
text = P(text)
roots = text.nth_root(2, all = True)
roots = [long_to_bytes(int(i)) for i in roots]
# 2 results

接着 我们逆向function函数

1
2
3
4
def inv_function(x,p):
    for i in range(0,256):
        if function(i,p) == x:
            return i

接下来只需要从终态出发，逆着走一遍过程即可，让G老师结合已有信息写了个脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
# solve.py
from Crypto.Cipher import AES
from Crypto.Util.number import long_to_bytes

# -----------------------------------------part 0: Setup and Constants----------------------------
a = [[239, 239, 251, 239], [233, 227, 233, 251], [251, 239, 251, 233], [233, 227, 251, 233]]
lis0 = [[341, 710, 523, 1016], [636, 366, 441, 790], [637, 347, 728, 426], [150, 184, 421, 733]]
lis1 = [[133, 301, 251, 543], [444, 996, 507, 1005], [18, 902, 379, 878], [235, 448, 836, 263]]
p_ = 71583805456773770888820224577418671344500223401233301642692926000191389937709
text = 26588763961966808496088145486940545448967891102453278501457496293530671899568
p_const_251 = 251

# -----------------------------------------part 1: Helper Functions----------------------------

def function(x, p):
    if x >= p:
        return x
    elif pow(x, (p - 1) // 2, p) == 1:
        return pow(x, 2, p)
    else:
        return pow(x, 3, p)

inv_function_cache = {}
def inv_under_function(y, p_mod):
    if (y, p_mod) in inv_function_cache:
        return inv_function_cache[(y, p_mod)]
    res = [x for x in range(256) if function(x, p_mod) == y]
    inv_function_cache[(y, p_mod)] = res
    return res

def bit_at(v, i):
    return (v >> (9 - i)) & 1

def tonelli(n, p):
    if pow(n, (p - 1) // 2, p) != 1: return -1
    if p % 4 == 3: return pow(n, (p + 1) // 4, p)
    Q, S = p - 1, 0
    while Q % 2 == 0: Q //= 2; S += 1
    if S == 1: return pow(n, (p + 1) // 4, p)
    z = 2
    while pow(z, (p - 1) // 2, p) != p - 1: z += 1
    c, x, t, m = pow(z, Q, p), pow(n, (Q + 1) // 2, p), pow(n, Q, p), S
    while t != 1:
        i, temp = 0, t
        while temp != 1: temp = pow(temp, 2, p); i += 1
        if i == m: return -1
        b = pow(c, 1 << (m - i - 1), p)
        x, t, c, m = (x * b) % p, (t * pow(b, 2, p)) % p, pow(b, 2, p), i
    return x

# -----------------------------------------part 2: Core Reverse Logic----------------------------

def build_prev_and_check(A_rc, aes_cipher, next_text):
    enc = bytearray(16)
    # 逆向 str_to_matrix: enc[r+4c] = inv_function(matrix[c][r], 251)
    for c in range(4):
        for r in range(4):
            pre_list = inv_under_function(A_rc[c][r], p_const_251)
            if len(pre_list) != 1: return None
            enc[r + 4*c] = pre_list[0]

    prev_text = aes_cipher.decrypt(bytes(enc))
    
    # 正向校验
    enc2 = aes_cipher.encrypt(prev_text)
    matrix_A_check = [[function(enc2[r + 4*c], p_const_251) for r in range(4)] for c in range(4)]
    matrix_B_check = [[function(matrix_A_check[c][r], a[c][r]) for r in range(4)] for c in range(4)]
    bts = bytes(sum([[matrix_B_check[r][c] for c in range(4)] for r in range(4)], []))
    
    return prev_text if bts == next_text else None

def invert_round(next_text, round_index, aes_cipher, lis_matrix):
    # 逆向 matrix_to_str
    M2 = [[next_text[row*4 + col] for col in range(4)] for row in range(4)]
    
    # 逆向 function 更新，并用 lis 过滤
    Cands = [[None]*4 for _ in range(4)]
    for r_B in range(4):
        for c_B in range(4):
            # 正向: B[r][c] = function(A[c][r], a[c][r])
            # 所以需要用 a[c_B][r_B] 来反解 M2[r_B][c_B] 得到 A[r_B][c_B] 的候选
            r_A, c_A = c_B, r_B
            cand = inv_under_function(M2[r_B][c_B], a[c_A][r_A])
            b = bit_at(lis_matrix[c_A][r_A], round_index)
            cand = [x for x in cand if (x > a[c_A][r_A]//2) == (b == 1)]
            if not cand: return None
            Cands[c_A][r_A] = cand
            
    # DFS回溯解决歧义
    A_rc = [[0]*4 for _ in range(4)]
    amb = [(r, c) for r in range(4) for c in range(4) if len(Cands[r][c]) > 1]
    
    # 先填充没有歧义的候选值
    for r in range(4):
        for c in range(4):
            if len(Cands[r][c]) == 1:
                A_rc[r][c] = Cands[r][c][0]

    if not amb:
        return build_prev_and_check(A_rc, aes_cipher, next_text)

    def dfs(k):
        if k == len(amb):
            return build_prev_and_check(A_rc, aes_cipher, next_text)
        r, c = amb[k]
        for v in Cands[r][c]:
            A_rc[r][c] = v
            res = dfs(k + 1)
            if res is not None: return res
        return None

    return dfs(0)

def invert_all_rounds(final_blocks, liss, aes_key):
    cipher = AES.new(aes_key, AES.MODE_ECB)
    blocks = [final_blocks[0], final_blocks[1]]
    for i in reversed(range(10)):
        print(f"  Inverting round {i}...")
        for t in (0, 1):
            nb = invert_round(blocks[t], i, cipher, liss[t])
            if nb is None: return None
            blocks[t] = nb
    return blocks[0] + blocks[1]

# -----------------------------------------part 3: Main Execution----------------------------

def main():

    key_int = 60679
    aes_key = long_to_bytes(key_int << 107, 16)

    # --- part 3.2: Find final state candidates ---
    r = tonelli(text % p_, p_)
    roots = [r, (p_ - r) % p_]
    candidates = []
    for s in roots:
        for k in (0, 1):
            v = s + k * p_
            if v < (1 << 256):
                candidates.append(v)

    # --- part 3.3: Run the reverse process ---
    for i, v in enumerate(candidates):
        print(f"\n[+] Testing final state candidate #{i+1}...")
        rb = v.to_bytes(32, 'big')
        final_blocks = [rb[:16], rb[16:]]
        res = invert_all_rounds(final_blocks, [lis0, lis1], aes_key)
        if res is not None:
            print("FLAG =", res.decode())
            return
            
            
if __name__ == "__main__":
    main()
    
# moectf{E@5Y_1eGendre_@nd_@ES*10}

End

时间过的好快啊 做题的时候似乎去年那个刚刚接触CTF，接触CS的自己就在眼前，页面还是一样的 机子还是一样的 已经从下不了手逐渐到现在的ak Crypto/Reverse了，或许从单纯的加分来说，CTF的获奖难度不算是什么很有”性价比”去值得做的事情吧，但是单纯享受密码学的优雅，享受用严谨的数学推导追根溯源的过程，有时候生活，学习不就是这些简单的正反馈支撑着我们一路走来嘛

Moe年年都在办 师傅们也是一轮一轮的换代 成长 DAWN2025的新生力量们非常强 这次合力打下了rk3 加油啊

一年能让人成长很多，期待下一个一年，祝moe和西电Sec越办越好！我们明年再见！